√ y=x2乗 171807-Y=x2乗+1 軸
Y X 2 2x 3の平方完成について X 2 2x 3 X 1 2 4 となったので 数学 教えて Goo
数学1aの質問です。 次の関数のグラフを書け。 y=x^24x3という問題です。 基礎問題精講の演習問題33(1)の問題で、グラフを書くことはできたのですが、範囲が分からず、解説の、x平方根の考え方を用いた解き方 x 2 = 数字 の形に式を変形できればxは右辺の 平方根 で表すことができる。 平方根とは ≫ (例1) A 2 = 3 A = ± 3 →Aの2乗が3なので、Aは3の平方根になる。 (例2) (x5) 2 = 3 x5 = ± 3 x = 5± 3 →( )の中身を一かたまりと考え、(例1)と同様にして、 →(x5)の2乗が3なので
Y=x2乗+1 軸
Y=x2乗+1 軸- 計算 y=x^2 y = x2の 0\leq x\leq 1 0 ≤ x ≤ 1 を下の式に代入します。 L=\displaystyle\int_ {0}^ {1} \sqrt {1 (2x)^2} dx L = ∫ 01 1 (2x)2dx ここで、根号を外すことを目標にして x=\displaystyle\frac {1} {2}\tan\theta x = 21 tanθ と置換する。 \displaystyle\frac {dx} {d\theta}=\displaystyle\frac {1} {2 26日前 スーパーカブ y=x2乗x のグラフ上に x 座標が 2 であるような点 A と, x 座標が 2h であるような点 D をとるとき, 以下の?に入力しなさい (i) AD の傾きを, h を用いた式で表すと abh （ a,b は定数）の形になります このとき b=?です
円の問題です どなたか教えて下さい 二つの円ｘ2乗 Y2乗 4ｘ 0 1 数学 教えて Goo
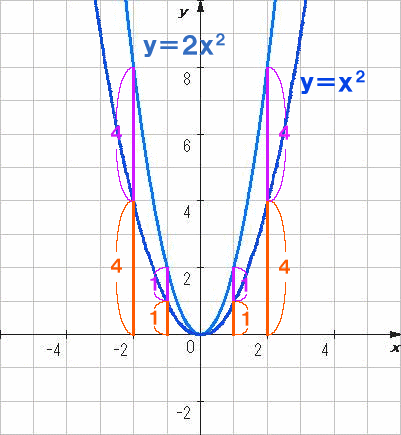
合成関数の微分公式と例題7問 レベル ★ 基礎 極限，微分 更新日時 この記事では 合成関数を微分する方法 を2通り紹介します。 合成関数の微分をマスターすれば y= (x^23x1)^4 y = (x2 3x 1)4 など複雑な関数も微分できます。 例題7問と3通りの証明 y=x2乗−2x5 平方完成は y＝a(xb)^2cにする事ですね 簡単なやりかたは微分することです。 これは頭の中でも出来ます y'＝2x2=2(x1) この時のy'=0 にするxを求めればよい。簡単でYがxの2乗に比例することが分かっている場合、 y = ax 2 にxとyの値を代入して比例定数を求めることができる。 1次関数とちがい、1点を代入するだけで式が出る。 yがxの2乗に比例し、x=2のときy=でした。このときのyをxの式で表す。 y=ax 2 にx=2, y=を代入すると
因数分解を行う式を電卓に入力し「因数分解」ボタンを押してください。 置き換えや公式を連続して使うなどの複雑な因数分解では途中式も表示されますので解き方の手順がわかります。 この電卓は中学で習う因数分解に対応しています。 3次式などの 1/2乗がルートと等しくなる理由 さてそれでは、本題の解説に入りましょう。 今はまだ がどういうものか分かっていません。 しかし、 が であることは分かるはずです。 なぜならばすでに、 「 の 乗の 乗とは、 の 乗に等しくなる」 という事が定め 0 この回答にコメントする あいす 5ヶ月前 どちらもy=なので、まとめるとy=x²=x2ということ。 よってx²=x2を解いてxを出し、どちらかの式にそのxの値を代入してyを出せばよい。 0 この回答にコメントする 回答するにはログインが必要です。
Y=x2乗+1 軸のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 授業実践記録 |  授業実践記録 |  授業実践記録 |
 授業実践記録 |  授業実践記録 |  授業実践記録 |
授業実践記録 |  授業実践記録 | 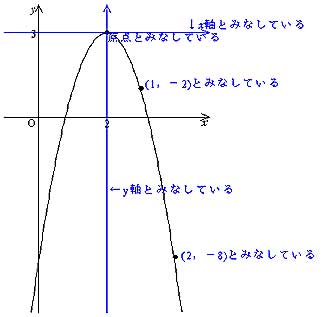 授業実践記録 |
「Y=x2乗+1 軸」の画像ギャラリー、詳細は各画像をクリックしてください。
 授業実践記録 |  授業実践記録 |  授業実践記録 |
 授業実践記録 | 授業実践記録 |  授業実践記録 |
 授業実践記録 |  授業実践記録 | 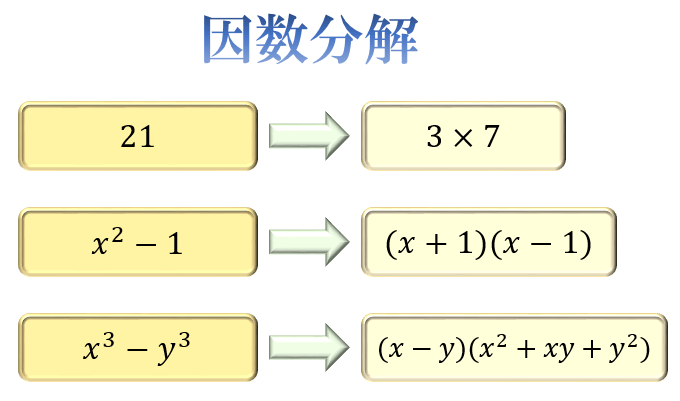 授業実践記録 |
「Y=x2乗+1 軸」の画像ギャラリー、詳細は各画像をクリックしてください。
 授業実践記録 | 授業実践記録 |  授業実践記録 |
 授業実践記録 |  授業実践記録 | 授業実践記録 |
 授業実践記録 |  授業実践記録 |  授業実践記録 |
「Y=x2乗+1 軸」の画像ギャラリー、詳細は各画像をクリックしてください。
 授業実践記録 |  授業実践記録 | 授業実践記録 |
 授業実践記録 |  授業実践記録 | 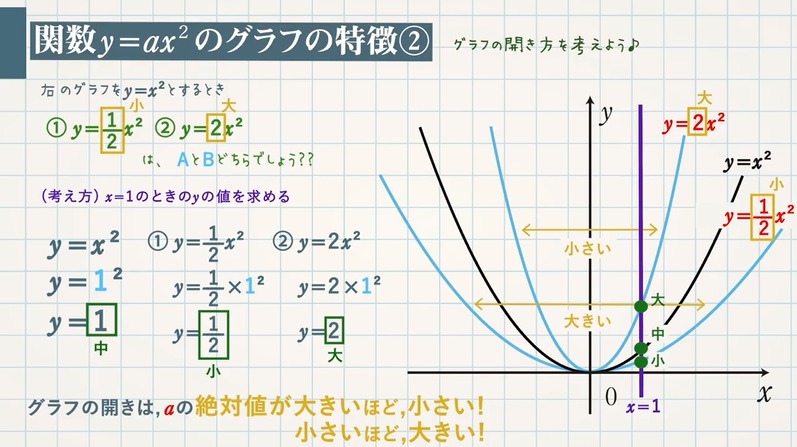 授業実践記録 |
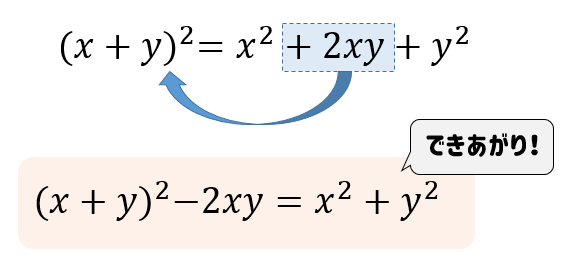 授業実践記録 |  授業実践記録 |  授業実践記録 |
「Y=x2乗+1 軸」の画像ギャラリー、詳細は各画像をクリックしてください。
 授業実践記録 | 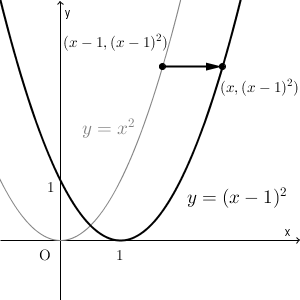 授業実践記録 |  授業実践記録 |
 授業実践記録 | 授業実践記録 |  授業実践記録 |
 授業実践記録 |  授業実践記録 |  授業実践記録 |
「Y=x2乗+1 軸」の画像ギャラリー、詳細は各画像をクリックしてください。
 授業実践記録 |  授業実践記録 |  授業実践記録 |
 授業実践記録 |  授業実践記録 |  授業実践記録 |
 授業実践記録 |  授業実践記録 |  授業実践記録 |
「Y=x2乗+1 軸」の画像ギャラリー、詳細は各画像をクリックしてください。
 授業実践記録 |  授業実践記録 | 授業実践記録 |
授業実践記録 |  授業実践記録 |  授業実践記録 |
 授業実践記録 |  授業実践記録 |  授業実践記録 |
「Y=x2乗+1 軸」の画像ギャラリー、詳細は各画像をクリックしてください。
 授業実践記録 |  授業実践記録 |  授業実践記録 |
 授業実践記録 |  授業実践記録 |  授業実践記録 |
 授業実践記録 |  授業実践記録 | 授業実践記録 |
「Y=x2乗+1 軸」の画像ギャラリー、詳細は各画像をクリックしてください。
 授業実践記録 | 授業実践記録 |  授業実践記録 |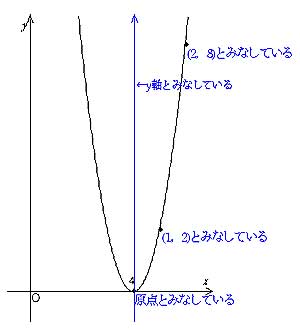
授業実践記録 |  授業実践記録 |  授業実践記録 |
 授業実践記録 |  授業実践記録 |  授業実践記録 |
「Y=x2乗+1 軸」の画像ギャラリー、詳細は各画像をクリックしてください。
 授業実践記録 |  授業実践記録 |  授業実践記録 |
 授業実践記録 |  授業実践記録 | 授業実践記録 |
 授業実践記録 |  授業実践記録 |  授業実践記録 |
「Y=x2乗+1 軸」の画像ギャラリー、詳細は各画像をクリックしてください。
 授業実践記録 |  授業実践記録 | 授業実践記録 |
 授業実践記録 |  授業実践記録 |  授業実践記録 |
 授業実践記録 |  授業実践記録 |  授業実践記録 |
「Y=x2乗+1 軸」の画像ギャラリー、詳細は各画像をクリックしてください。
 授業実践記録 |  授業実践記録 | 授業実践記録 |
 授業実践記録 |  授業実践記録 |
関数 について、 の値が2から4まで増加するときの変化の割合を求めなさい。 変化している の値に注目して、それらの値を足します。 そして、この値に比例定数を掛けます。 今回の問題であれば2ですね。 という感じで、一瞬で計算することができます
Incoming Term: y=x2乗, y=x2乗+1 グラフ, y=x2乗+1 頂点, y=x2乗+1 平方完成, y=x2乗+1 軸, y=x2乗+2x グラフ, y=x2乗-3 グラフ, y=x2乗-4x+3, y=x2乗-4x+3 グラフ, y=x2乗 頂点,
コメント
コメントを投稿